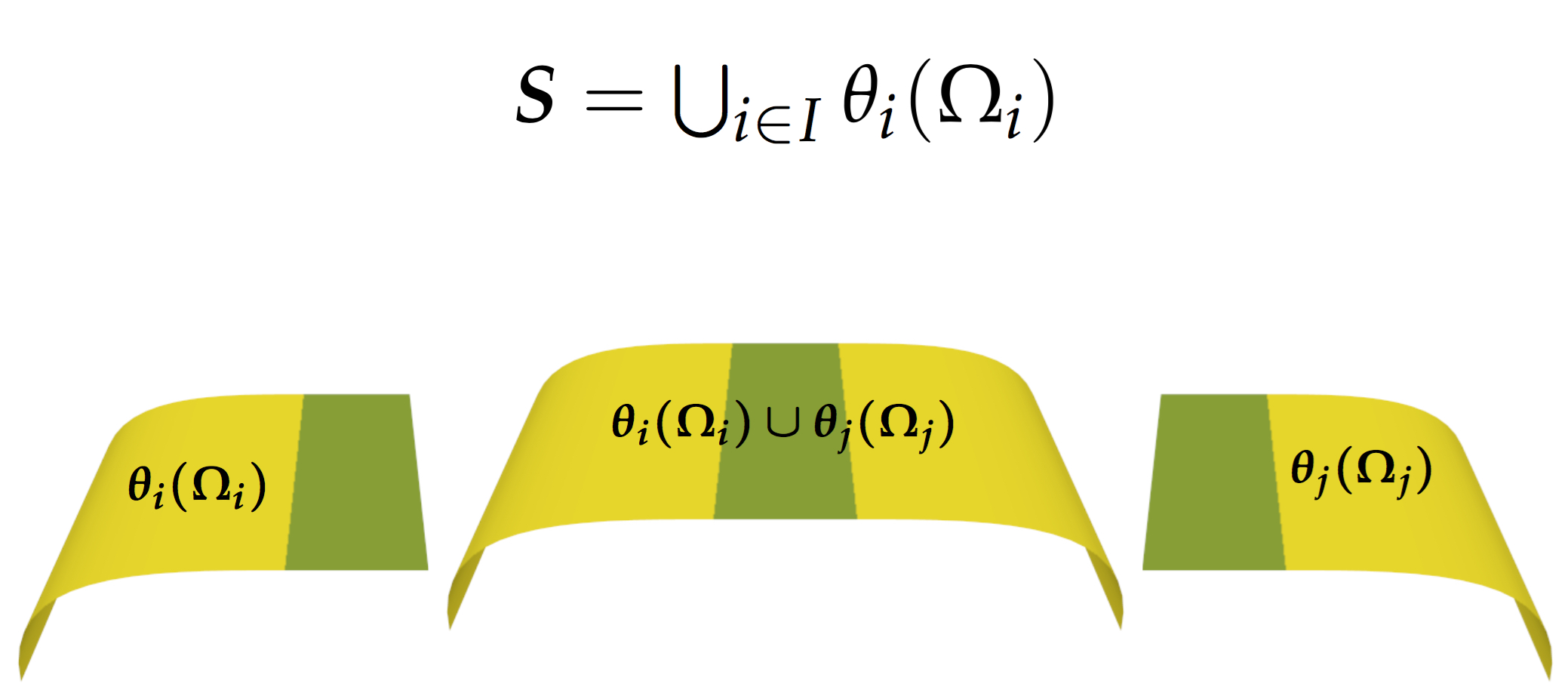Research Projects |
|
|
|
|
Characterization of aquifers through computational methods - Nov/2012 to Dec/2016 |
|
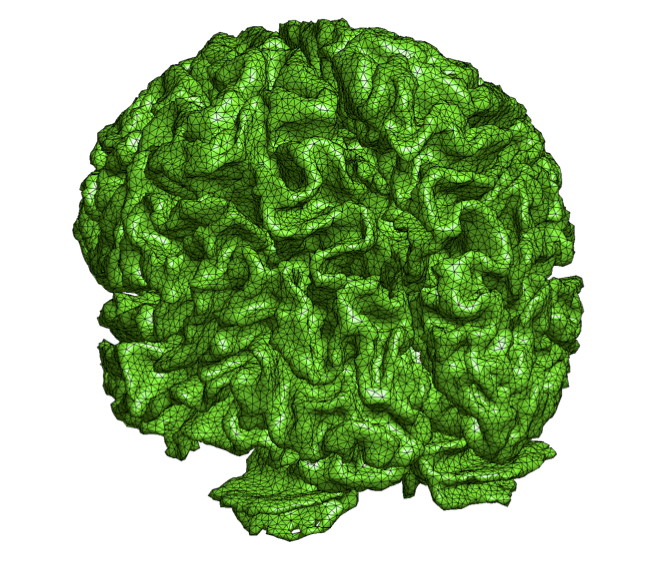
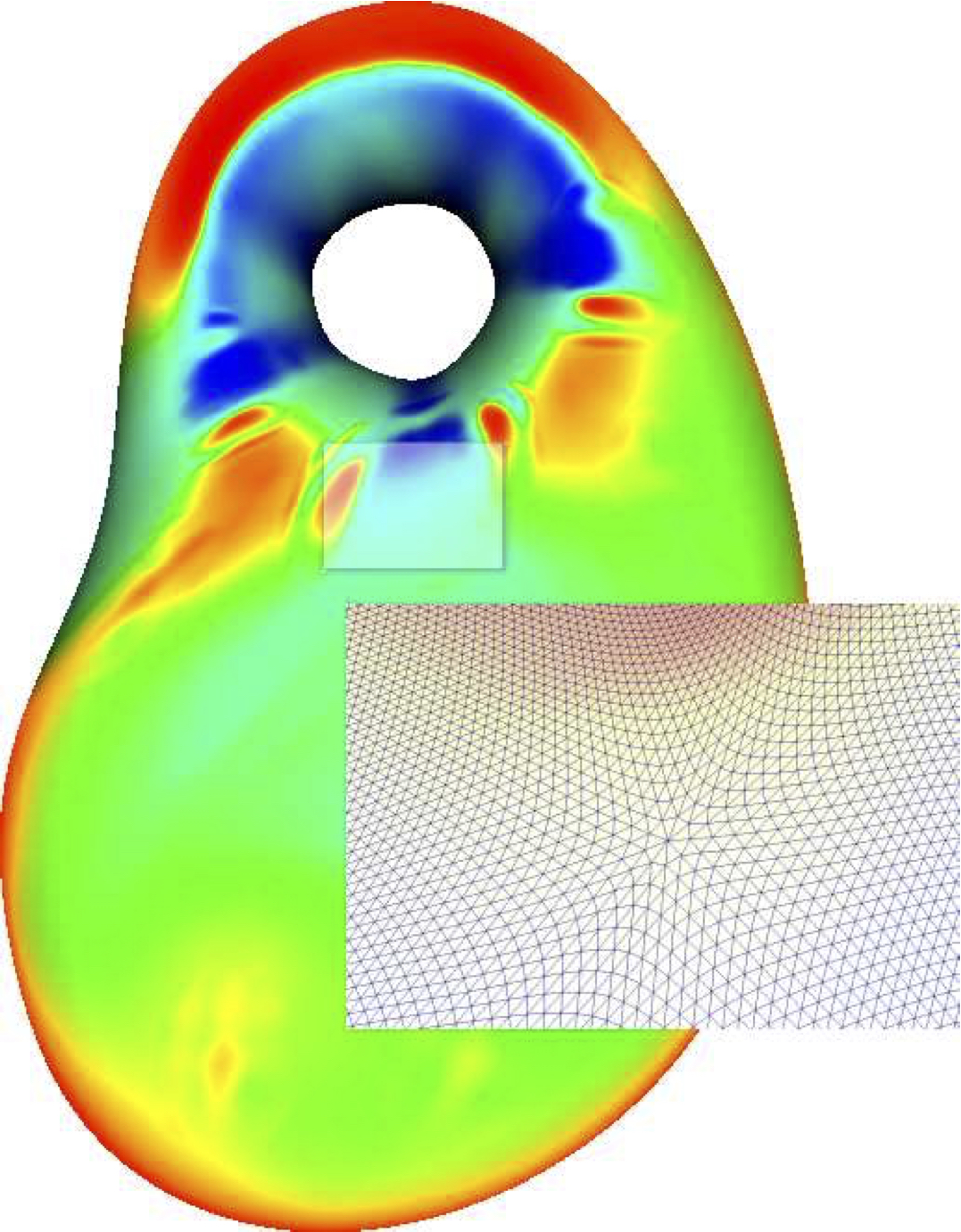
This project is interdisciplinary. It requires expertise from hydrogeology, image processing, percolation theory, mesh generation, high performance computation, and computational fluid dynamics. The goal of the project is the development of a computer system to estimate porosity, intrinsic permeability, and hydraulic conductivity of aquifers from 2D images of thin sections obtained from rock samples. These physical quantities allow us to characterize aquifers, which store groundwater for domestic consumption, agriculture and industry. More importantly, the proposed computer system allows us to measure those physical quantities without the need for drilling wells, reducing costs and risks of water contamination. The system will have immediate application to the characterization of Aquifer Barreiras, which is responsible for the water supply of over 80% of the entire population of the east coast of Rio Grande do Norte state, Brazil, and for which there are no consistent data available. The proposed computer system computes the aforementioned physical properties using a very similar methodology to the one described in this paper. Roughly speaking, we first generate a volumetric image from a set of 2D images of thin sections obtained from rock samples. Next, we generate a tetrahedral mesh from the volumetric image. Finally, we run a numerical simulation that simulates water flowing through the porous media (represented as a tetrahedral mesh) according to Darcy's Law. I am the Principal Investigator (PI) of the project. My involvement with the technicalities of the project is limited to the mesh generation and fluid flow simulation stages. Mesh generation is a central theme of my research, and this project has given me the opportunity to revisit the problem of generating provably good meshes from imaging data. The project team consists of several senior researchers, namely: Dr. Leandson Lucena (DGEF-UFRN), Dr. Bruno Motta (DIMAp-UFRN), Dr. Afonso Paiva Neto (ICMC-USP), Dr. Paulo Pagliosa (FACOM, UFMS), Dr. Sidarta Araújo (DMAT, UFRN), and Dr. Mario Costa Sousa (UCalgary, Canada). Dr. Leandson Lucena and Dr. Bruno Motta have been advising some undergraduate and graduate students working on the project. CNPq, one of the main Brazilian research funding agencies, has been funding the project since November 2012 (R$ 120.000,00 -- one hundred twenty thousands reais). Computational resources allocated to the project team have been acquired with these funds, and they are mostly located at Imagina Research Lab at UFRN. The project activities are expected to end in December 2016. Publications, softwares, reports, theses, etc, produced as results of the project will be made available in this page as soon as the project ends. |
|
|
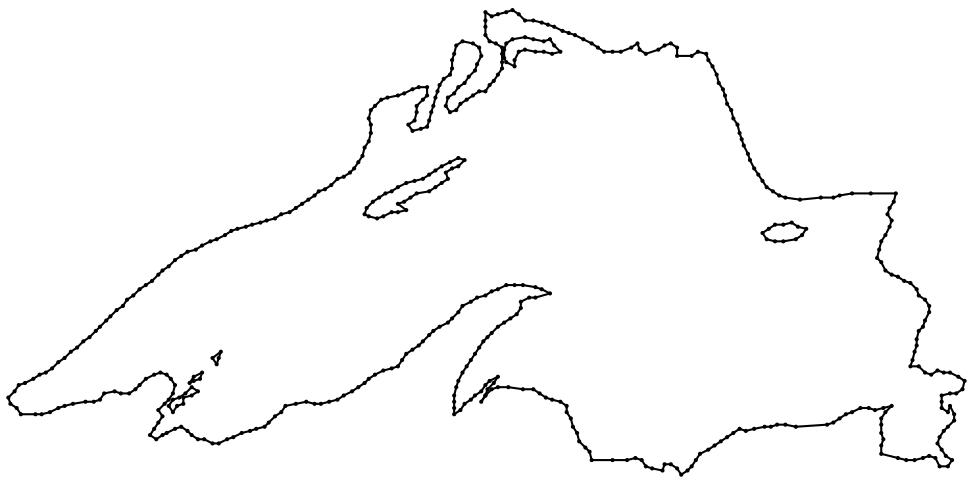
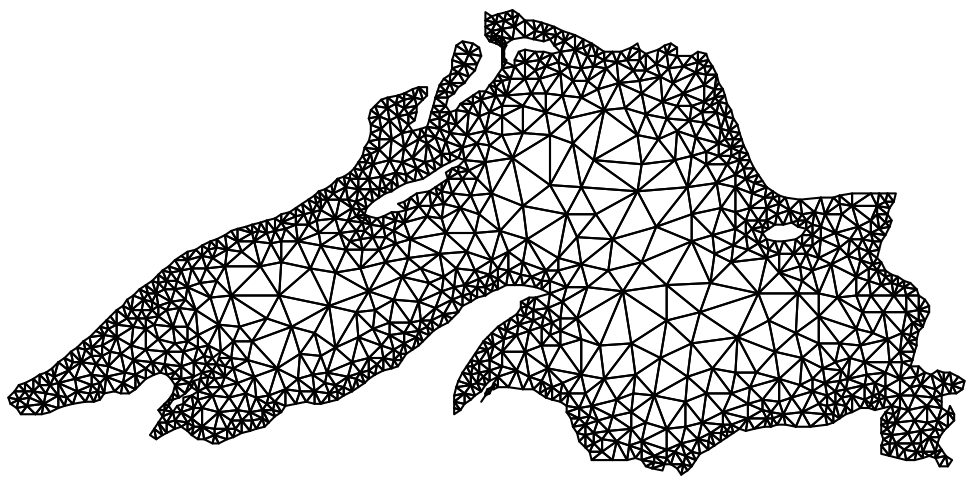
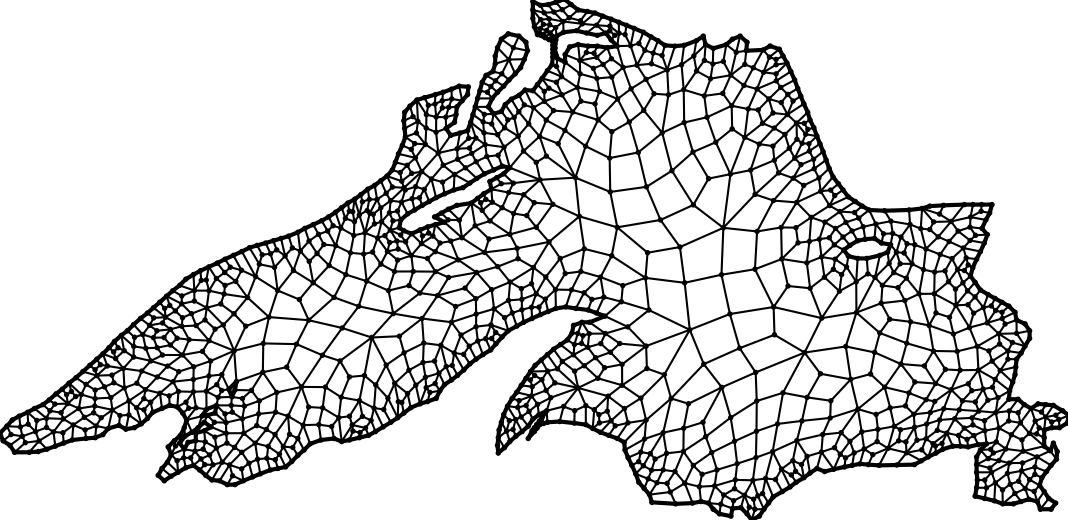
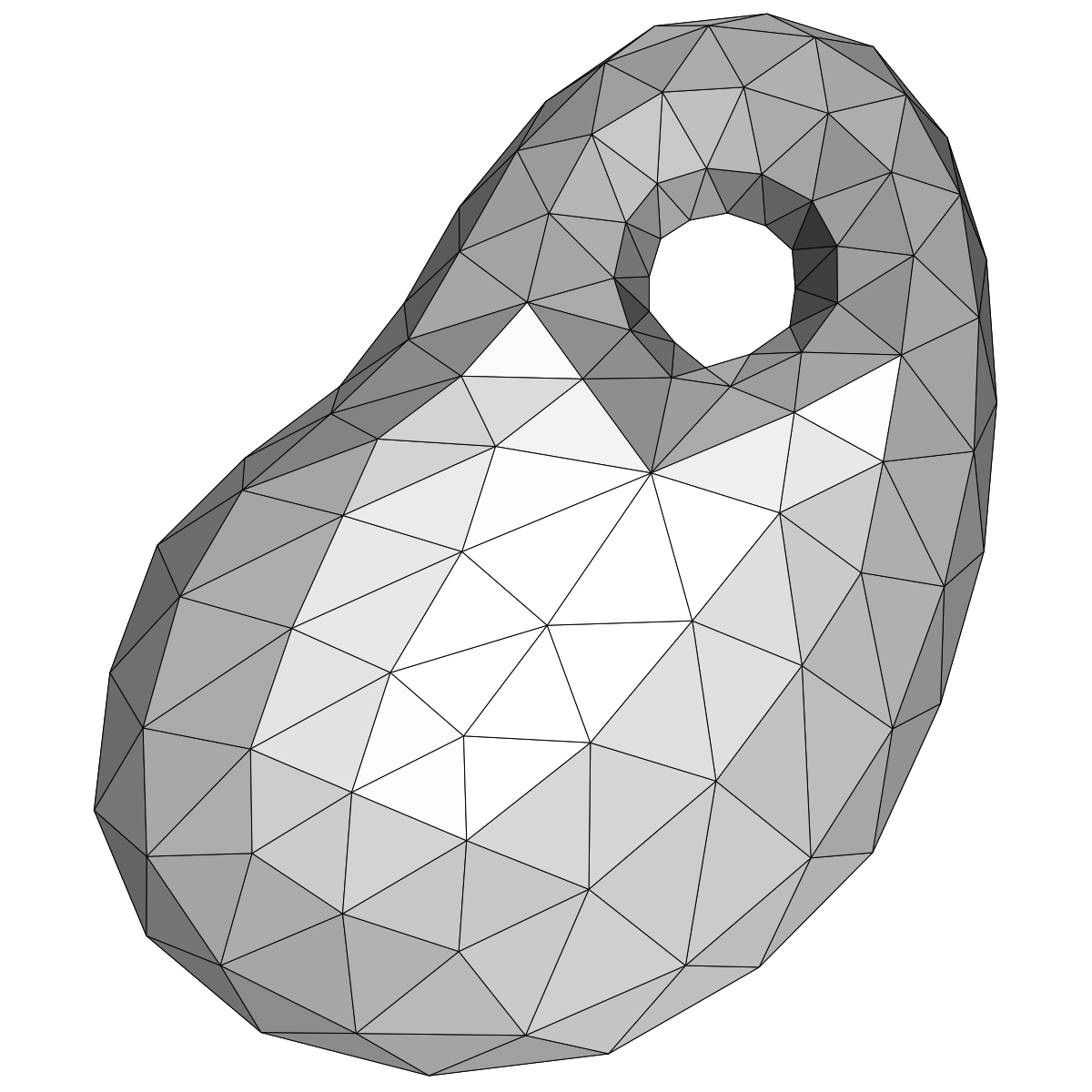
Mesh generation from imaging data - Aug/2000 to Jul/2008A mesh is a decomposition of a geometrical domain into smaller and simpler geometric shapes (called elements) such as triangles and quadrlaterals (if the domain is planar - 2D) and tetrahedra and hexahedra (if the domain is spatial - 3D). Meshes are ubiquous in applications from various fields of knowledge. In geography and cartography, meshes are used to interpolate height maps of terrains, to produce maps, and to generate contours and topographic views. In computer graphics, objects are in general converted into a mesh before the rendering operation takes place. Moreover, polygonal meshes have now become the de facto standard representation form of graphics objects. Finally, meshes are also necessary in almost all applications that rely on multivariate interpolation. In particular, the generation of a mesh of the problem domain is a prerequisite for the use of the Finite Element Method (FEM), which is one of the most powerful and popular numerical methods for solving partial differential equations (PDE) in variational form. The accuracy and precision of the numerical solution of a PDE produced by the FEM, together with the time taken to obtain the solution, are highly dependent on mesh parameters such as number and shape of the elements, and regularity, directionality and adaptivity of the mesh. The main goal of this project is two-fold. First, I wanted to devise and implement mesh generation algorithms that are guaranteed to produce meshes of good quality with respect to optimal values of the mesh parameters. Second, the algorithms should be able to handle imaging data (i.e., objects represented by 2D and 3D binary images). The first contribution of this project was a meshing algorithm for converting triangle meshes into quadrilateral ones. The algorithm is guaranteed to produce meshes of bounded size. An implementation of this algorithm is freely and publicly available for download. Below you see an image of a quad mesh generated by the algorithm:
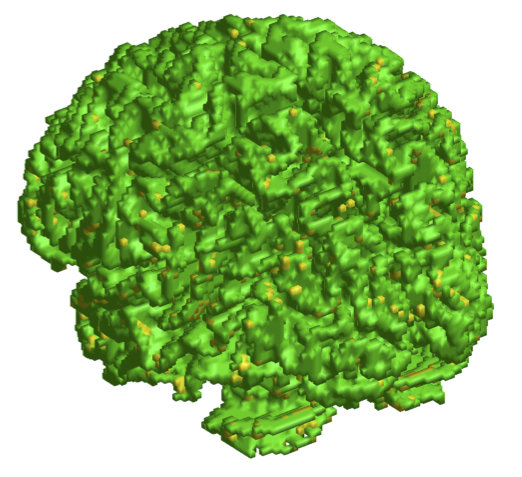
Later, I devised and implemented an algorithm for generating provably good quality triangle surface meshes from 3D binary images. The distinguishing feature of the algorithm is the fact that it makes use of two representations of the "surface" to be meshes: a digital representation and a continuous one (i.e., a smooth surface). To make sure that both representations are consistent, I converted the input binary image into a well-composed one. The operations executed by the algorithm are based on either representation. The choice is based on efficiency and numerical robustness. More recently, I have found a better "continuous" representation for the surfaces to be meshes, and I am currently working on a better version of my surface meshing algorithm (as part of another project). More details on the algorithm can be found in my thesis and in my publications. Below you see the digital representation of a 3D binary image and the corresponding mesh generated by my surface meshing algorithm:
The project started during my Ph.D. studies at the University of Pennsylvania. It was funded by CNPq, one of the main Brazilian research funding agencies, from 2000 to 2004, and then from 2006 to 2008. During those two periods, I collaborated with some researchers on the theoretical aspects of both algorithms I developed, namely: Dr. Suneeta Ramaswami (Rutgers Univ., USA), Dr. Longin Latecki (Temple University, USA), Dr. Jean Gallier (UPenn, USA), Dr. James Gee (UPenn, USA), and Dr. Nicholas Tustison (Univ. of Virginia, USA). My quadrilateral meshing algorithm was also used by a finite element-based image registration method developed by Dr. Gee. |
|
|
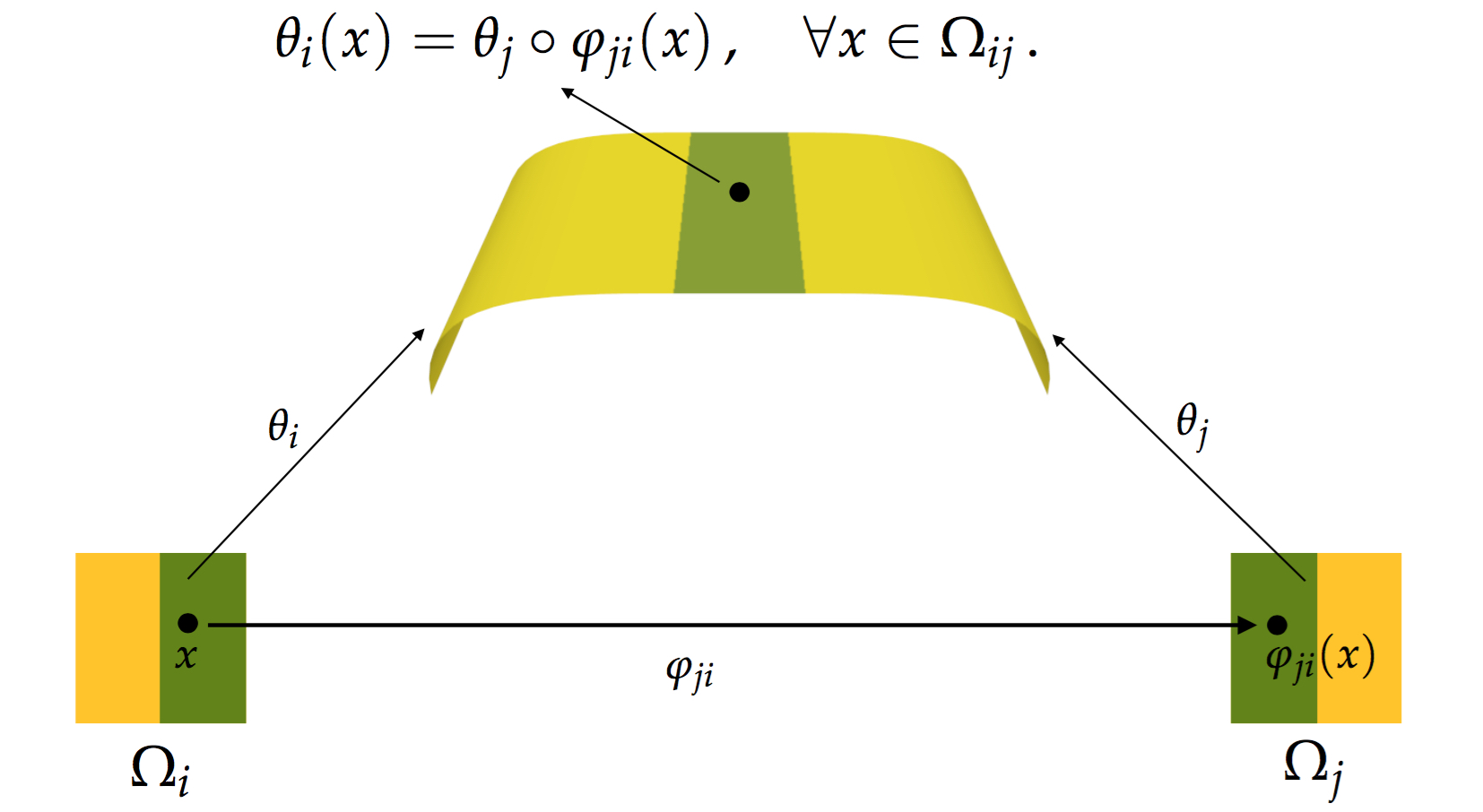
Parametric pseudo-surfaces - Nov/2009 to Jul/2017Parametric pseudo-surfaces are smooth surfaces defined by a set of local parametrizations from the Euclidean plane to the Euclidean space. The image of each parametrization is a surface patch homeomorphic to an open disk in the Euclidean plane. Two or more patches can overlap, and the set of all patches define a surface cover.
The surface itself is the union of all patches:
PPSs can be easily defined from triangle meshes. The mesh topology can be used to define which patches overlap, while the mesh geometry (i.e., the vertex coordinates) can be used to define the surface shape. In principle, however, PPSs can be constructed from different data modalities (e.g., point sets and multiple view images).
The approach underlying the construction of PPS's is known as the manifold approach, and it was pioneered by Cindy Grimm and John Hughes. The main advantage of this approach is the ease with which it enables us to define Ck-continuous surfaces (i.e., the PPSs), for an arbitrary k. In 2008, some colleagues and I devised a new construction of PPS's based on the manifold approach, and since then we have worked on applications that can benefit from PPS's built by our construction (e.g., optimization of mesh parametrization, texture synthesis and fluid flow simulation, to name a few). You can find more information about PPS's in this course. You can also download my code for constructing and sampling PPS's from triangle meshes. Along the last 8 years I have collaborated with several people on various developments of our new manifold-based construction of PPS's: Dr. Jean Gallier (UPenn, USA), Dianna Xu (Bryn Mawr College, USA), Dimas Martínez Morera (DM-UFAL, Brazil), Luis Gustavo Nonato (ICMC-USP, Brazil), Luiz Velho (IMPA, Brazil), and Esdras Medeiros (DM-UFC, Brazil). From 2010 to 2013, CNPq funded the project. Results from applying PPS's to optimization of mesh parametrization, texture synthesis and fluid flow simulation will be posted here as soon as the project ends. |
|
|
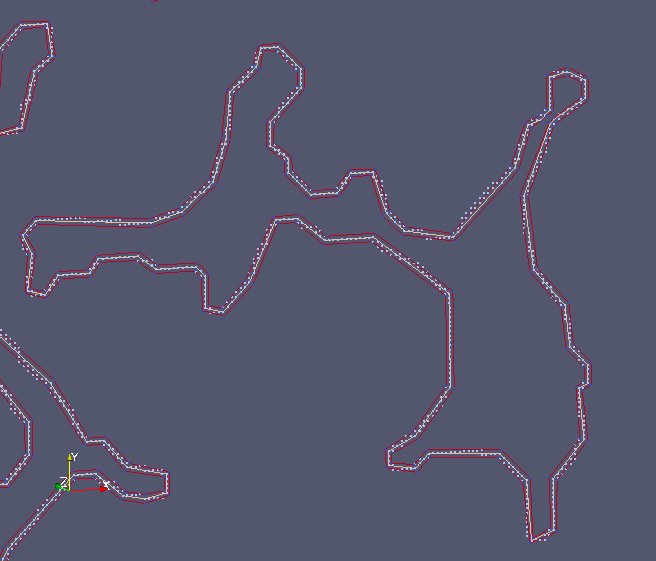
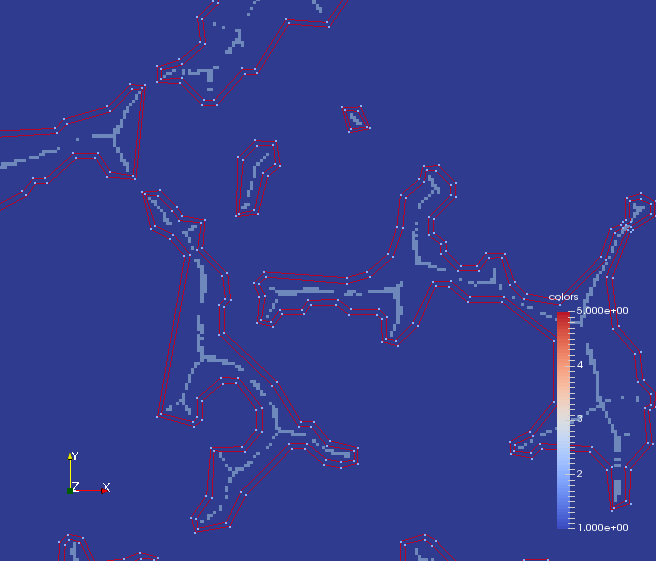
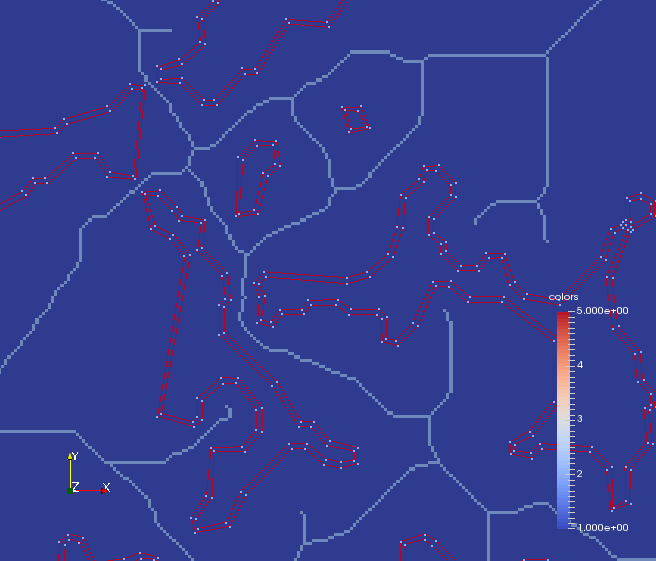
Smooth curves from 2D well-composed, binary images - Aug/2015 to Jul/2016A 2D binary image is well-composed if and only if the continuous analog of the digital boundary between the foreground and background of the image is a one-dimensional manifold (i.e., a curve). Roughly speaking, this manifold is the piecewise-linear curve consisting of the edges and vertices share by the pixels that separate the foreground and background of the image. In general, if the object represented by the image foreground has a smooth boundary, this piecewise-linear curve is not a good approximation to the boundary. The reason is that the curve has a jaggy appearance. For an application such as meshing, a jagged boundary can have a negative impact on both the performance of the meshing algorithm and on the mesh quality. In this project we aim at defining smooth curves that approximate the jagged piecewise-linear curves corresponding the continuous analog of the digital boundary between the foreground and background of a given well-composed image. Our approach builds a channel around the continuous analog (CA) of the digital boundary between the foreground and background of the image. More specifically, the CA is first simplified using a slight variation of the Ramer-Douglas-Peucker (RDP) line simplification algorithm. Then, a channel is defined by offsetting the simplified line along its (opposite) normal directions (see figures below). The main challenge is to ensure that the channels corresponding to separate curves do not intersect with each other.
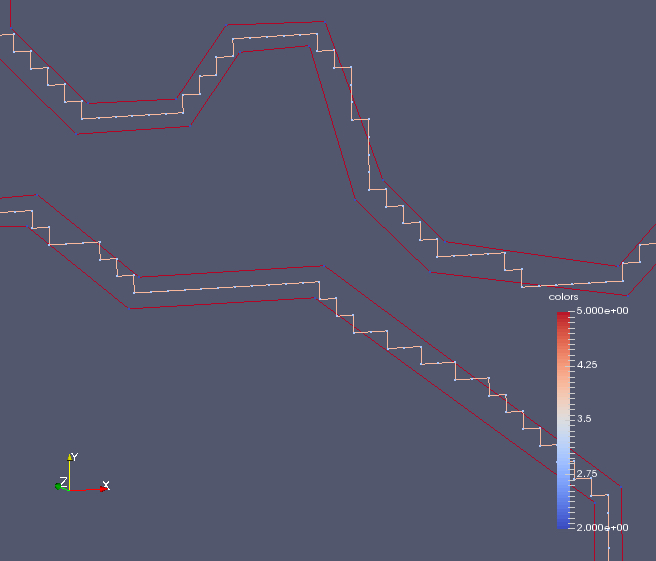
The channel does not have to contain the vertices of the CA (see figures in the top row below). But, the distance from every vertex of the CA to both piecewise-linear envelopes of the channel is guaranteed to be within a prescribed bound. To ensure this distance bound and that the channels do not intersect each other, we use the distance transform of the given well-composed image as well as the distance transform of approximations to the skeletons of the image background and foreground (see figures in the bottom row below).
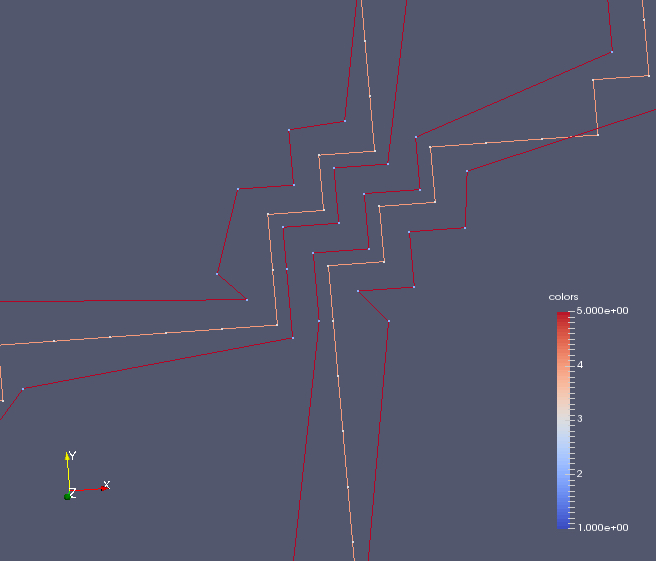
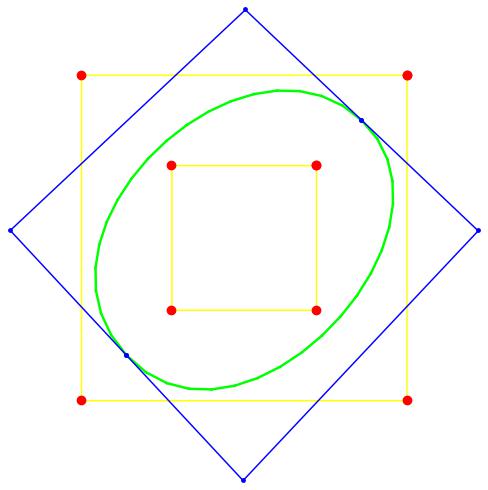
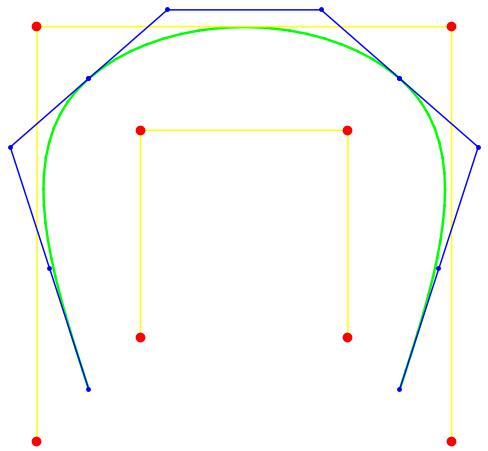
Once the channels are built, we thread a smooth curve into each channel. Each curve is a B-Spline of degree 3. The degree can actually be arbitrary, but the curves are used by a new meshing algorithm that requires curves that are curvature-continuous everywhere. To thread the curves into channels, we solve the channel problem as described by Lutterkort and Peters (see figures shown below). Since the channels do not intersect each other, neither does the curves that reside inside them. Therefore, each smooth curve approximates a unique piecewise-linear, jagged curve of the set of curves of the CA, and the former is also topologically equivalent to the latter curve.
The project is funded by CNPq. My only collaborator in this project is Dr. Jörg Peters (University of Florida, USA). Code from this project shall be available in this page soon. For the time being, you can play with a simple C++ program to thread a C1 spline curve into a channel. The code that builds the C2 spline curves used by the project is similar. |
|
|
|
Last update: March 13, 2016 |