Digital Topology and Geometry |
|
|
|
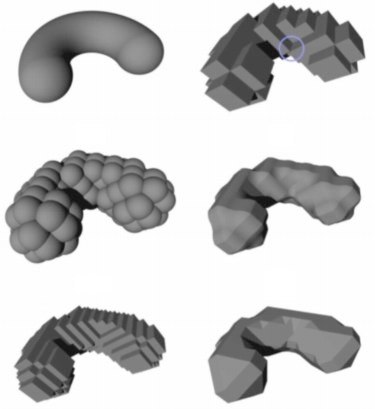
I became interested in digital topology and digital geometry by chance. When I was a Ph.D. student (back in 2000), I tackled the problem of generating meshes from imaging data, which is still a central theme of my current research. At the time, I noticed that most algorithms for creating meshes from images either work directly on the digital data or convert the digital data into another representation form before meshing the data. Algorithms that convert the data before meshing in general discard the digital data afterwards. Since several operations can be carried out more efficiently on digital data, I thought that it would be useful to keep both representations. But, to that end, the representations should be "consistent". Unfortunately, even when the object from which the imaging data was generated is a "manifold", the digitization process may not preserve the object topology. To make things worse, the correct topology cannot be recovered from the digital data if no additional information is provided (which is the most likely scenario in practice). When the digital data is converted into another representation form, the latter is in general a manifold whose topology is not always equivalent to the one of the digital data. A typical example is the Marching Cubes algorithm for extracting polygonal surfaces from 3D binary images. The polygonal surface may not have the same topology of the continuous analog of the digital boundary between the foreground and the background of the image when the latter is not a manifold. In this case, the two representations (the digital data and the polygonal surface) are not topologically equivalent. As a result one cannot interchange between them when operating on the data. During the development of my Ph.D. thesis, I came accross a paper by Longin Latecki on the characterization of binary images whose continuous analog of the digital boundary between the foreground and the background of the image is always a manifold: the so-called well-composed images. So, I decided to develop an algorithm for repairing images that are not well-composed, so that they become well-composed. This algorithm provided me with a way of perturbing binary images to ensure "manifoldness", which ultimately allowed me to convert the digital data into a topologically equivalent piecewise-linear representation of the data. Therefore, I could consistently interchange between representations when operating on the data for efficiency purposes. Below, you find some of my papers related to digital topology and digital geometry. Currently, I am not tackling any problem in this area. |
|
|
|
Tustison, N.; Avants, B.; Siqueira, M.;
Gee, J.
|
|
|
|
Siqueira, M.; Latecki, L. J.; Tustison, N.;
Gallier, J.; Gee, J.
|
|
|
|
Stelldinger, P.; Latecki, L. J.; Siqueira, M.
|
|
|
|
Last update: March 13, 2016 |